In CircleCI, a Rails app used Ubuntu to run its test suite. Jenkins ran the lighter Alpine docker container with the same code. Some specs failed, but the most interesting contained the following error message:

expected: 6.551163549203511
     got: 6.551163549203513

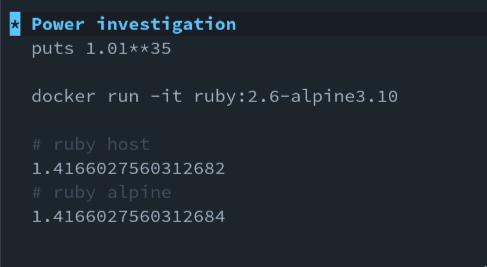
By comparing multiple math operations one by one in order, I found the culprit: The result of 1.01**35 was 1.4…*2* in Ubuntu and my local machine, and Alpine resulted in 1.4…*4*. One ended with two, and the other ended with four. Interesting.

# Ubuntu
>> 1.01**35
1.4166027560312682

# Alpine
>> 1.01**35
1.4166027560312684

To unblock me, I changed the test to ignore that precision. The feature didn't require it, and the test needed to pass on other devs' machines. In the end, it's not rocket science that will cost the company $500 million.

# Before
expect(score).to eq 6.551163549203513

# Fix the issue
expect(score).to be_within(0.1).of(6.5511)

I was curious and copied this calculation snippet to a personal note for later investigation. I am, many years later, trying to find out what is happening.

A computation could theoretically perform this exponentiation operation at several abstraction levels. Let's investigate these layers, from low-level to high-level, so we have a place to look for them.

• CPU: Maybe, it's implemented directly as an instruction on the CPU. But, as far as I know, no chip brings a POW instruction, only ADD, MUL, etc. So, not here. Besides, Circle CI and Jenkins were on x86, so no different Floating-point unit either.
• linux kernel: It is not happening here as well. Kernel mantainers even discourage operations with floating-point inside the kernel. Even if a syscall existed for that, paying the performance price would be demanding for a computation that could happen in userspace. Take this quote from Linus:

the rule is that you really shouldn't use FP (Floating-point) in the kernel. There are ways to do it, but they tend to be for some real special cases

• libc: The libc is a library of standard functions, for example, a memory allocator exposing malloc and free APIs, syscall wrapping and other common operations. One of them is the pow function from math.h. The header file specifies the operation as double pow(double x, double y), and the linker points to this implementation on compilation time to build the final executable. This way, C programs, like Ruby, don't need to reinvent the wheel.
• standard library: Some languages implement this operation themselves and don't rely on any libc at all. For example, Golang has this option (unless using cgo), so it must implement exponentiation itself.

Influenced by Smalltalk, all Ruby types are objects, even a class. It wouldn't be different for Float. These objects can receive and pass messages to each other.

>> 1.01.class
Float
>> 1.01 ** 35
1.4166027560312682
>> 1.01.**(35)
1.4166027560312682

On the other hand, languages taking a more "functional" approach have a Math.pow-like function that receives two numbers as arguments.

Let's dig a bit deeper and see the bytecode of this operation:

>> puts RubyVM::InstructionSequence.compile('1.01**35').disasm
== disasm: #<ISeq:<compiled>@<compiled>:1 (1,0)-(1,8)> (catch: FALSE)
0000 putobject                              1.01                      (   1)[Li]
0002 putobject                              35
0004 opt_send_without_block                 <calldata!mid:**, argc:1, ARGS_SIMPLE>
0006 leave

YARV (Yet another Ruby VM) is a stack-based virtual machine. First, The VM calls the method ** on the last popped object (1.01). Then, Ruby defines the ** method for Float by forwarding it to the rb_float_pow C function. At the end of it, the line: return DBL2NUM(pow(dx, dy)); uses the pow function from libc.

We found out that the issue lies in the libc. Ubuntu uses the ubiquitous glibc, while Alpine ships with the lightweight-alternative musl. They have completely different implementations. Golang also had the same result as glibc in the alpine image, so it's definitely musl.

Let's isolate this to a docker image.

FROM alpine:latest

RUN apk --no-cache add ruby

ENTRYPOINT ["ruby"]

When running this today with docker run <id> -e 'puts 1.01 ** 35', I receive the number with 2 in the end, just like Ubuntu. Uh-oh. What's going on? Was it all a dream, maybe?

Travelling through musl git history, I can see that a commit replaced the previous algorithm to use what's on arm-optimized-routines. I didn't find the exact motivation in the mailing list for the reason changed that, but my assumption is to improve performance. The old logic still prints the different value when pointing to an old Alpine version (at least 3.10).

As a sidenote, the original C file had two interesting statements in the initial comment section:

1. The algorithm results in nearly rounded numbers. So musl returning a different value from glibc is not a bug, according to my newbie interpretation,
2. Alpine devs got this code from FreeBSD at the beginning of the project. I don't know the exact motivations, but maybe FreeBSD matched the BSD license from musl, while glibc is using the LGPL license. By the way, this "broken" value is still present in FreeBSD 13.

Floating-point calculations are always tricky. Doing exponentiation with them is a recipe for imprecision. I'm still curious about what's different with the FreeBSD algorithm. But musl and glibc sharing values since 2019 don't motivate me enough to investigate it. This fact, and debugging 300 lines of cryptic math operations, is not what I consider a fun side project for Saturday.

Anyway, I hope you enjoyed reading how a software error caught me by surprise 👋.